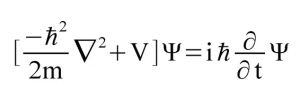Smoke and Mirrors

I have been interested in quantum stuff ever since I started talking maths with the Arts people after I hit bottom . They took it as a mission to stop me from being black-and-white but then they were also fascinated as to how far science went. At that time scientific destruction was begun with wonderful books like "The Dancing Wu Li Masters" by Gary Zukav, and "The Tao of Physics" by Fritjov Capra. Both of these writers have gone on and done stuff, but they are not central or mega-significant in terms of the establishment, yet their ideas should be. HHDL's Mind and Life might have that mantle now but again it is not mainstream.

On my journey I picked up a book called "The Quantum and the Lotus" by Matthieu Ricard and Trinh Xuan Thuan. It appears to be conversations between a biologist who became a monk and a Buddhist scientist, certainly a useful arena for the Path of Scientific Enquiry. And on page 9 I stopped reading because something Thuan said "Is ... a science in the same sense as a natural science - that is to say, based on observation, with maths as its language?" I was at the beach, and I knew it was important so I let it sink in.

This morning I woke up and I'm not doing stuff for 3 days, and my mind won't stop - I forced myself to meditate because I wanted my mind clear. But I couldn't so gave up. Thuan is talking of a wonderful compartmentalisation in science/academia that hides a multiplicity of "stuff", and disguises the delusions that are accepted. And when we are looking at quantum stuff with their absurdities these delusions are much more significant. Sheldrake talks about the 10 core assumptions in science, but those assumptions I have described as "hidden science" because as Sheldrake points out these assumptions are not discussed.

But maths is based on assumptions. What Thuan said is a fair assessment of science's approach physical observation based on the language of maths. So science is based on the assumptions of maths - apart from "hidden science".

Schrodinger's equation is an important equation of quantum stuff and I have no idea what it means.



This looks a fascinating and powerful equation to me - I mean it. But it has two things in it that rings the bells of assumptions to me "i" and partial differentiation - limiting behaviour.

I am going to use the "i" and wander into complex numbers.

Complex numbers. But first let's get a grip on number because number is quite arbitrary even though as a building brick of maths it is considered solid. A number doesn't exist - OK less dramatic they are not real. A number only makes sense as a descriptor - 3 apples, but what has happened through the centuries and agreements made in school in maths classes we all have an agreed sense of what 3 is. Because we all use it the same way we don't question what is involved in its usage. It makes sense to use it the way we do but it is full of agreed assumptions and we don't question it.

But this screen is a 14 inch long. No it isn't. It is about 14 inches long. To be correct, from corner to corner the screen is about 14 inches, maybe between 13.8 inches and 14.2 inches. But then 13.8 and 14.2 have their own accuracy measures - maybe 13.75 to 13.85 and 14.15 to 14.25. So the screen is more accurately described as 13.75 to 14.25, then 13.745 to 14.255, then 13.7445 to 14.2555, and so on. All of this as people we call 14, as mathematicians we call it assumptions. Reasonable assumptions but still assumptions. In most situations the number 14 suffices because we all agree what it means but on occasions these assumptions really matter.

Take a spark plug. Let's suppose the gap in the spark plug is supposed to be 1.4 mm, and 1.42555 is too big and it won't fire. Then these type of apparently pointless assumptions do matter. In what I am considering overall, what really matters is that assumptions are made - even with the simple use of numbers, and we have to evaluate these assumptions.

So I come back to Thuan's comment. Science does not in general evaluate mathematical assumptions it compartmentalises those assumptions and relies on the mathematicians - the language of science.

Let's look at another aspect of number - Dedekind cuts. How many numbers are there between 0 and 1? 10? 0.1, 0.2, 0.3, ... 0.9, 1.0. 4? 1/4, 1/2, 3/4, 1. OK. Let's take 10. How many numbers are there between 0.1 and 0.2, and the answer could be 10 again. 0.11, 0.12, ... 0.19, 0.2. And how many between 0.11 and 0.12? 10? 0.111, 0.112 ... 0.119, 0.12. Each of these cuts produces "ten" more numbers. So if you are "anal" enough to ask the question how many numbers are there between 0 and 1, then you are anal enough to accept the answer infinity. For most people and situations the question is totally meaningless. Are all these numbers fractions or decimals?

There are numbers - we call them irrational numbers, that cannot be written as fractions or decimals. The easiest one to get our heads around is SQRT(2), this is the number that solves the equation x² = 2 (x = SQRT(2)). But what is SQRT(2)? 1.42 = 1.96. 1.4142 = 1.999396, and 1.4152 = 2.002225. Now we can get as close to 2 as we want but it will never exactly equal 2 because "2 does not exist or 2 is not real". So we invent a number called SQRT(2) whose square is exactly 2. But SQRT(2) cannot be written as a fraction or a decimal. What is the area of a circle? πr². Simple? Take the radius, let's say 4cm, square it 16 cm². Multiply by π, whatever that is - press the button on the calculator or use whatever is given in the question 3.14, 3.142, 3.14159265359. In school to avoid a multiple of answers the question usually says 2 decimal places - helps the marker!!! But in truth the area of a circle also has an infinite number of answers - Dedekind cuts. But we have a convention - an agreement - that there is one answer.

So between 0 and 1 we have an infinite number of numbers and some of those numbers are irrational 1/SQRT(2), 1/π, and so on. So when we have a number system we have many many assumptions that people don't usually consider.

In some ways maths gets harder in school as it gets further and further away from what makes common sense. Early on in secondary school we get introduced to negative numbers. At this stage we have been taught numbers without all the assumptions (of Dedekind cuts, irrational numbers, infinite possibilities for lengths or areas). The number 3 is an accepted "reality" so then mathematicians ask what is x if x+3 = 0? From a mathematician's point of view this is a very sensible question, pushing back the boundaries of mathematical questioning in the hope of coming up with a sensible answer that might prove useful.

The answer of course is -3, equation solved. Maths as language can be used in science as -3. So what are we doing? Measuring a length of -3 cm? Counting -3 apples? No -3 is just something we use in maths, and most people accept -3 is a number. But it exists even less than any other numbers. 3 apples can be counted but 3 is a descriptor and it has no existential meaning. If I went to ask for -3 apples, they'd lock me up. But most people are happy to accept that -3 exists.

In the spirit of mathematical enquiry we give negative numbers rules, addition, subtraction, multiplication and division. Cos that's what mathematicians do. How can you add two things that don't exist? Everywhere in the world if you asked people to add -2 and -3 you will get the answer -5 - except for kids in my classes Why? Then we get a teacher's trick. Draw a number line -5, -4, -3 ... 3,4,5. Go to -2 and go to the left a further 3 and you get -5. So let's call this -2 + -3, and get the answer -5.

So there is some kind of physical interpretation we can use here - the number line. So what happens if we try to multiply -2 x -3? Kids will usually say -6 to begin with. That would make intuitive sense, and the teacher says they are wrong -2 x -3 is +6 because --=+. Why? A physicist might then say two negative things attract and become positive, but isn't it more sensible to go with what the kids say -6? After telling the kids many times, and making them fail tests if they go with intuition, we get the agreement that -x- = +, and -/- = +.

We have made agreements based on assumptions that mathematicians have made. And we have begun to get into interesting quantum territory with some of these assumptions. How many numbers between 0 and 1? Infinite. That's absurd. We can have some kind of notional concept of fractions - 1/2 a cake, 0.1 is a tenth of an inch, but what the hell is an irrational number? And if there is such a thing as an irrational number what is the point? I can see some point in 3 apples, 1/2 a cake, a 1/10 of an inch, but what is an irrational number? Yet we can use π to find areas of circles - it has a practical use.

But then what's the use of negative numbers? They're unreal. But then because we accept the definition of multiplication we can make them real by squaring them -3*-3 = 9 and we can have 9 apples.

So by examining numbers we can see that there are all kinds of assumptions. And importantly we take a rule for negative numbers that is not perhaps intuitive, and we can make negative numbers "real" by squaring them. It works. And this is an important assumption for quantum theory, and it is an assumption that most kids do not at first find intuitive.

We then get further intuitive errors:- x² = 9, so x=3. As a maths teacher I have to mark this wrong - absurd, maybe I give half marks. Now that we have negative numbers the answer is that x = -3 or +3, without taking -3 as a possible answer there are situations of practical relevance that would not be included - sorry can't think of one but they are there.

By accepting negative numbers we can introduce a practical situation that we all accept. We have already seen a number line with negative numbers but what about graphs what do they mean?



And then we get



for some reason -x and -y have not been marked.

But we know all this, it is real. Now I hope you will start to say, it is not real it is just part of what we assume. Number is riddled with assumption but it works especially if we go to school get rid of intuition and accept the rules and conventions and make an agreement.

So maths enquiry said great, we have come with the answer to the question x² = 9 as +3 or -3, so now how about answering this equation x² = -4? So we are looking for a number which when we square it gives a number that doesn't exist. Here is what maths did. They said that -4 can be written as -1x4 so if we take the square root we get SQRT(-1) and SQRT(4). We now accept that SQRT(4) is +2 or -2, but what do we do with SQRT(-1)? What's the square root of something (-1) that doesn't exist? Everybody calls it "i". So the answer to the question x² = -4 every mathematician and scientists accepts as +2i or -2i.

Here's the rub. This "i" is an assumption about an assumption, and it is arrived at by a rule that -x- = +. And it is arrived at by an assumption that it is reasonable to say that we can have a thing called i where i² = -1.

And where do we find i? In Schrodinger's equation.



Here is what I feel about this. I can accept numbers as existing such as 1,2,3 ... These are natural (they are actually called natural numbers). Between 1 and 2 there are an infinite number of numbers some of which are irrational. Absurd. Then we extend to negative numbers there is some kind of intuitive acceptance when we see negative as meaning go back or go down on axes:-



But this is just a way of explaining, it isn't "real" - although maths people call these axes of real numbers.

But then we get to "i" imaginary numbers. We even draw axes for these, and give it a "funny" name - Argand diagram - to make them look as if they exist.



But imaginary numbers are invented to make calculations about something that is made up (i= SQRT(-1)) about something (-1) that is made up. And yet Thuan has happily compartmentalised his observation so long as there is mathematical language, and has compartmentalised the assumptions. I am not having a pop at Thuan, I could have said the "natural sciences".

What is wonderful about imaginary and negative numbers is that if you are using equations all you have to do is square them and they become real. i² = -1 and (-1)² = 1. To make imaginary stuff real all you have to do is square them. When you look at the development of maths it all seems perfectly reasonable, I want to solve x+3 = 0, I want to solve x² + 4 = 0 so I invent numbers and rules. But what you have done is use maths to make imaginary stuff real.

Now making imaginary stuff real normally seems a waste of time. When little kids come up with imaginary friends we find the nicest way we can of telling our kids that they don't exist, they're not real, and we basically find a nice way of getting rid of them. However making imaginary stuff real in maths is useful. Somehow Schrodinger's equation helps quantum scientists predict quantum events, and as with quantum computing these quantum events happen - they are real.

But what we are talking about is a whole bunch of imaginary assumptions. I have no problem with accepting quantum events such as superposition and entanglement as happening. I am quite happy to accept that mathematicians far far far far more capable than I - great respect - are able to manipulate things such as Schrodinger's Equation so that there is some element of prediction that is practically useful. But it is all assumption, assumption that has a mathematical integrity but nevertheless assumption.

So am I doing a "fake news" on science? In a way only, because a scientist should always be sceptical. Where are scientists going with quantum theory? They are trying to talk about stuff they cannot see. What they can observe is effects and in the sub-atomic arena there is some pretty weird stuff such as superposition and entanglement. What they are looking at however has practical applications, and this is important. So science turns to maths as if it is the sacrosanct language. But maths is stack full of assumptions. Are these assumptions invalid? Certainly not as far as I know, but in the sub-atomic arena we must contend the possibility that the maths of normal space might fall down. What is normally seen as the "laws of physics" is definitely out of the window.

But I am not trying to dispute the maths. 0² = 0, and if we take that new zero and square it again we have zero. If we start with nothing and keep squaring it we get nothing. Somehow we start with i, square it and we get -1, and square that we get +1. We start with the imaginary and we get the real. If that happened anywhere else other than maths we would laugh it out of the window.

Maths is a logical language, its sphere of influence is logic yet it is being used in the arena of the absurd to substantiate the absurd. You do not substantiate the absurd by logic or we could not have superposition. Here is what I am saying. It is the observation that is substantive, scientific verification through mathematical derivation is not appropriate, this is not a world of reason and logic. Accept the observation, use the maths to help validate the observation, don't use a discipline that is based on assumptions that might well not apply in the quantum arena.

I am not asking you to refute the observation, the observation can be repeated. But when you look at aspects of knowledge which have been observation-based and reject them because they don't have the scientific verification of mathematical rigour, then consistently you should reject quantum physics.